東海大学湘南キャンパスに出張で行ってきた。
時間が少し余ったので生協で本を見ていたら、「オイラーの贈物」という本が目に入った。以前、本屋で見かけたことがあったけど、難しそうな印象があったのでスルーしていた。しかし、実際に手にとって内容を見ると数学の入門書的な内容だった。二度の絶版を経て、東海大学出版会で新装版として2010年に発行されている。ちょうど東海大学の生協でこの本に出会ったのは何かの縁を感じた。
ところで、オイラーの式というのは以下の様な式だ。
e^iθ = cos θ + i sin θ
特にθ = πのとき
cos θ = -1, sin θ =0なので
e ^iπ = -1
振動の微分方程式を解くときに出てくるので、なじみのある人も多いと思う。sin x, cos x, e^xのマクローリン展開を眺めていると、直感的にオイラーの式がなりたつことはわかるのだが、単振動の解がしっかりsin, cosと結びつき振動しそうな雰囲気を持っていることに魅力を感じる。
よくよく観察すると、(sin θ)' = cos θ, (cos θ)' = - sin θという具合にサインとコサインは循環しているという点。(e ^λx)' = λ・e^λx, (e ^λx)'' = λ^2・e^λxと、何度微分しても自分自身の関数形を維持し続けるe^xは類似している。
わかってそうでわかってないような消化不良感が残る。
eはネイピア数といい以下の式で定義される。
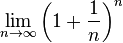（Wikipediaより）
実数で表すと、e = 2.718281828・・・・の無理数だ。学校で「鮒、ひと鉢、ふた鉢」と習った記憶がある。こんな式がなんでsin, cosと簡単な関係でつながっているのか、不思議だなぁと事あるごとに感じるので、もう少し深く知ってみたいと思う。
この本はオイラーの式を理解することを目的に、数学の基礎的な知識を学んでいくような構成になっていて、数学の専門家が読むような難解な数学書ではない。むしろ、高校くらいの数学の知識で読める。
オイラーの式を理解するためには、数や数の計算、方程式、微分、積分、テイラー展開、指数関数・対数関数、三角関数などの知識が必要なので、基礎的な数学を復習するのに興味深いアプローチができると思う。
数学のおもしろさを味わいながら、丁寧に読んでいこう。
～～～～
この本の最初の方に出てくる話題をひとつ。
0.99999・・・・= 1
この式、納得できる？レーテン、キューキューキュー・・・と１は違うじゃん。だって、レーテンキューキューキューって1じゃないし・・・。なんとなく、そう思う。
しかし、この本では次のような解説がある。まず、A = 0.33333・・・について考える。
A = 0.333333・・・
これを両辺を10倍すると、
10A = 3.33333・・・・= 3 + A
つまり
9A = 3
したがって
A = 1 / 3
A = 0.33333・・・・だったのでつまり、
0.33333・・・・= 1 / 3
両辺を3倍すると
0.99999・・・= 1
が得られる。
なんてことはない、1÷3が1 / 3（３分の１）と同じであると考えるなら1 / 3 = 0.33333・・・で、1 = 0.99999・・・に決っている。無限に１に近い数は１そのものに等しい。これは実数が途切れなく続いていることを意味している。
